Triangles on the Same Base and between the Same Parallels
Triangles on the Same Base and between the Same Parallels: Overview
This topic covers concepts, such as, Triangles on the Same Base and Same Parallels, Area of Triangles on the Same Base and between the Same Parallels, Triangles with the Same Base and Same Area & Area of Parts of Triangle Divided by a Median etc.
Important Questions on Triangles on the Same Base and between the Same Parallels
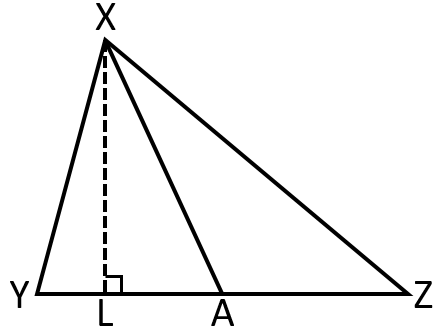
In , is a median on side. Find ratio of .
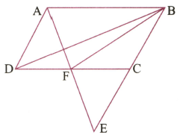
In Figure shown below, ABCD is a in which BC is produced to E such that . AE intersects CD at F. If area, find the area of the parallelogram ABCD.
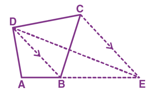
In a , and are respectively the mid points of and and is the mid point of . Then if Then equals
In a , and are respectively the mid points of and and is the mid point of . Then
The perimeter of a right angled triangle is . If its hypotenuse is then area of this triangle is
In the given figure, and is the mid point of . If , then find the value of .
In figure shown below, CE is drawn parallel to diagonal DB of a quadrilateral ABCD, which meets AB produced at E. Prove that ADE and quadrilateral ABCD are equal in area.
In figure shown below, a point E is taken on the side BC of a ABCD; AE and DC are produced to meet at F. Prove that areaarea.
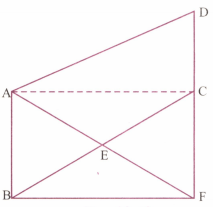
In figure shown below, a point E is taken on the side BC of a ABCD; AE and DC are produced to meet at F. Prove that area area
In figure shown below, point divides the side of a in the ratio , Prove that area : area .
A point E is taken on the side AB of the parallelogram ABCD, and the lines DE and CB are produced to meet at F. Prove that the triangles FDB and FEC are equal in area.
The vertex A of a triangle ABC is joined to a point D on the side BC. The mid points of AD is P. Prove that the area of triangle BPC is half the area of triangle ABC.
. If DC and BE meet at O, prove that and are equal in area.
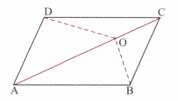
ABCD is parallelogram. O is any point on the diagonal AC. Show that area of is equal to the area of .
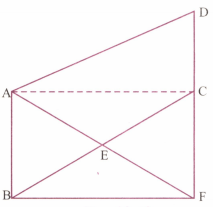
In Figure shown below, . Point E is the mid point of CA and CA. Prove that area area.
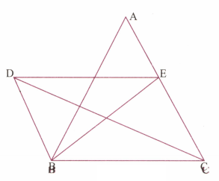
If the mid points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral.
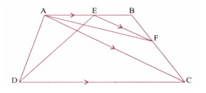
In Figure shown below, a trapezium ABCD has sides AB and CD parallel. A straight line parallel to the diagonals AC cuts AB at E and BC at F. Prove that triangles AED and ACF are equal in area.
In Figure shown, P and Q are points on the side AC of the such that . Through P, a line is drawn parallel to AB to meet BC at R. Prove that area area .
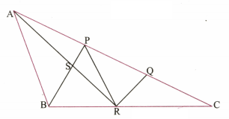
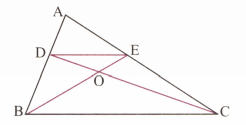
The medians BE and CF of a intersect at G. Prove that area area of quadrilateral AFGE.
If each diagonal of a quadrilateral divides it into two triangles of equal area, then show that the quadrilateral is a parallelogram.
